Analyzing Lagrangian coherent structures in water around swimming fish reveals how they move and may help in the study of airplane flight dynamics and other complex fluid flows
From the Journal: Chaos
WASHINGTON, D.C., June 23, 2015 — Fish may seem to glide effortlessly through the water, but the tiny ripples they leave behind as they wriggle their way along are evidence of a constant give-and-take of energy between the swimmer and its aqueous environment — a momentum exchange that propels the fish forward but is devilishly tricky to quantify because of the continuous nature of a large, ever-flowing body of water.
When dealing with discrete objects it is relatively easy to compute the force that each exerts on the other. Imagine a cross-country skier propelling herself across a field using ski poles. The skier and her poles are discrete objects, and we can relatively easily compute the forces they exert on each other. But since the water around a swimming fish is continuous, it can be hard to pick out which regions of the fluid are most relevant for propulsion.
Now, a group of Swiss scientists has found that a fish’s propulsion through water can be understood by studying vortices in the surrounding water as individual units instead of examining the flow as a whole. Their technique, published June 23 in the journal Chaos, from AIP Publishing, could also be useful in other fluid dynamic analyses — for example, when studying unsteady vortices detaching from the wing of an airplane.
In a series of modeling experiments, the researchers focused on the swirls in the water nearest to the fish. “These vortices are believed to play a crucial role for the propulsion mechanism of fish. The fact that they rotate is already a clear indication that the fluid has strongly interacted with the fish,” said Florian Huhn, the lead researcher on the project.
The researchers identified discrete vortex regions in the water by detecting and tracking shapes called Lagrangian coherent structures — regions of a flow field that undergo similar experiences. Specifically, they looked at regions where the fluid formed discrete vortices — that is, places where the water moved in a self-contained pattern such that, if one were to draw an invisible loop around it, no material would cross that line.
“The closed line engulfs the fluid inside the vortex,” said Huhn. “Once we find this closed boundary, we trace back the whole fluid patch inside and can observe how it contributes to the propulsion mechanism of the fish.” Identifying these structures within the fluid makes them into a discrete space whose forces can be more easily calculated.
The team simulated these flow fields for two different types of swimming. The first was a steady movement, characterized by regular undulations. The second was an escape response known as the C-start, in which the fish quickly curves into a “C” shape before flipping outwards and propelling itself rapidly forward.
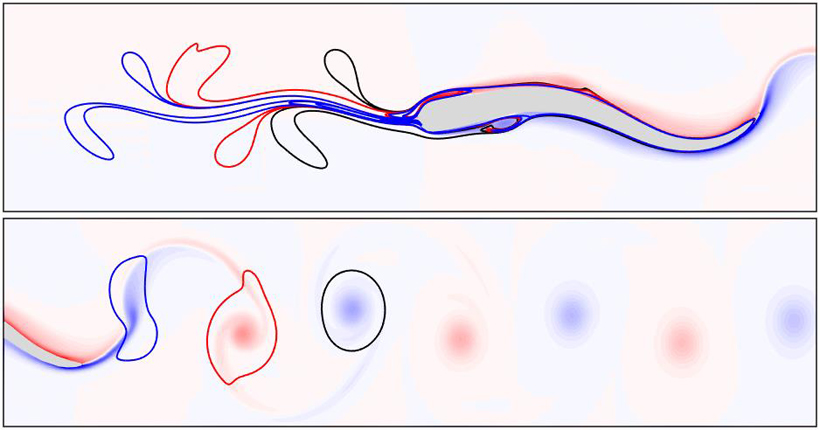
The researchers found that for a steadily swimming fish, the fish’s movement can be largely attributed to momentum exchange between the fish and the discrete vortices.
For the C-start response, the vortices also explained a large part of the motion, but “an additional non-rotating jet fluid region enclosed by the vortex region is found to be crucial for the propulsion,” said Huhn.
Huhn believes that his methodology may be useful in future fluid analyses as well. “Whenever a body propagates through fluid at a certain speed, be it birds and fish in nature or planes and ships in engineering, vortices are created, and the presented method can be used to track and understand the formation and evolution of the vortices,” he said. “Our findings further support the usefulness of Lagrangian coherent structures to decompose unsteady fluid flows into dynamically different regions.”
###
For More Information:
Jason Socrates Bardi
jbardi@aip.org
240-535-4954
@jasonbardi
Article Title
Quantitative flow analysis of swimming dynamics with coherent Lagrangian vortices
Authors
F. Huhn, W.M. van Rees, M. Gazzola, D. Rossinelli, G. Haller and P. Koumoutsakos
Author Affiliations
ETH Zurich, Switzerland; Harvard University, Cambridge, Mass.
